/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 5776325

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 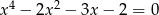4 2 x − 2x − 3x − 2 = 0 .

Rozwiązanie

Szukamy najpierw pierwiastków całkowitych wśród dzielników wyrazu wolnego, czyli wśród liczb -2,-1,1,2. Łatwo sprawdzić, że 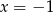x = − 1 jest pierwiastkiem. Dzielimy wielomian przez dwumian 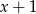x+ 1 . My zrobimy to grupując wyrazy.

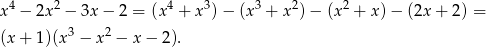
x4 − 2x2 − 3x − 2 = (x 4 + x 3)− (x 3 + x 2)− (x 2 + x )− (2x + 2) = 3 2 (x+ 1)(x − x − x − 2).

Ponownie szukamy pierwiastków całkowitych. Tym razem pierwiastkiem jest 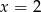x = 2 . Dzielimy wielomian stopnia 3 przez dumian x− 2 .

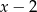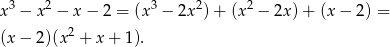
3 2 3 2 2 x − x − x − 2 = (x − 2x )+ (x − 2x) + (x − 2) = (x − 2)(x 2 + x + 1 ).

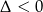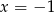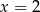Trójmian kwadratowy w nawiasie nie ma pierwiastków (Δ < 0 ), więc x = − 1 i x = 2 są jedynymi pierwiastkami.  
Odpowiedź: 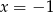x = − 1 lub x = 2

Wersja PDF