Zadanie nr 6050858
Wyznacz te wartości parametru 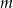 , dla których równanie
, dla których równanie 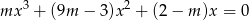 ma co najmniej jedno rozwiązanie dodatnie.
ma co najmniej jedno rozwiązanie dodatnie.
Rozwiązanie
Jedno rozwiązanie widać od ręki: 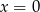 . Jak podzielimy równanie przez
. Jak podzielimy równanie przez  zostaje nam równanie
zostaje nam równanie
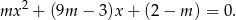
Jeżeli równanie to jest liniowe (dla 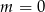 ) to mamy
) to mamy
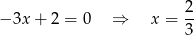
i jest OK.
Jeżeli 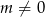 , to sprawdźmy kiedy równanie ma pierwiastki
, to sprawdźmy kiedy równanie ma pierwiastki
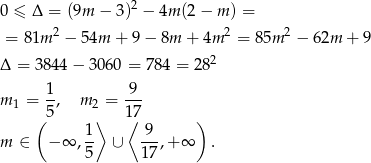
Sposób I
Jeżeli 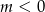 to ramiona paraboli
to ramiona paraboli 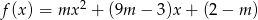 są skierowane w dół i będzie ona miała dodatni pierwiastek o ile
są skierowane w dół i będzie ona miała dodatni pierwiastek o ile 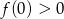 , lub gdy równanie ma pierwiastki (nierówności wyżej) i wierzchołek paraboli jest na prawo od 0. Sprawdźmy kiedy
, lub gdy równanie ma pierwiastki (nierówności wyżej) i wierzchołek paraboli jest na prawo od 0. Sprawdźmy kiedy 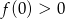 .
.
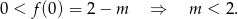
W ten sposób nie musimy nic więcej sprawdzać, bo widać, że dla wszystkich 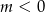 jest OK.
jest OK.
Jeżeli 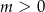 , to równanie będzie miało dodatni pierwiastek jeżeli
, to równanie będzie miało dodatni pierwiastek jeżeli 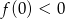 , lub gdy równanie ma pierwiastki (nierówności z
, lub gdy równanie ma pierwiastki (nierówności z 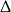 -ą) i wierzchołek jest na prawo od 0. Sprawdźmy kiedy
-ą) i wierzchołek jest na prawo od 0. Sprawdźmy kiedy 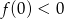
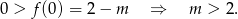
Sprawdźmy jeszcze kiedy 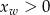
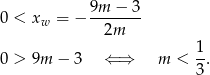
W połączeniu z nierównością na 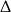 -ę mamy w tym przypadku
-ę mamy w tym przypadku 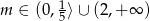 .
.
Podsumowując obie możliwości, rozwiązaniem jest zbiór
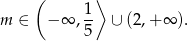
Sposób II
Tym razem użyjemy wzorów Viète’a. Mamy dwie możliwości: musimy mieć dwa pierwiastków różnych znaków (czyli 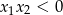 ), lub jeden z pierwiastków jest dodatni, a drugi nieujemny (
), lub jeden z pierwiastków jest dodatni, a drugi nieujemny (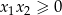 i
i 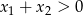 ). Pierwsza możliwość daje nam
). Pierwsza możliwość daje nam
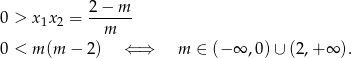
W połączeniu z 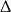 -ą daje to przedziały
-ą daje to przedziały 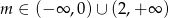 .
.
Sprawdźmy teraz drugą możliwość. Nierówność 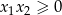 da nam przedział
da nam przedział 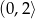 , a nierówność
, a nierówność 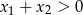 daje
daje
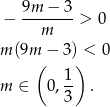
W połączeniu z warunkiem na 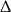 -ę mamy więc
-ę mamy więc 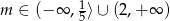 .
.
Odpowiedź: