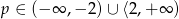/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 6258301

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane jest równanie 2 2 (x + 3)[x + (p + 4)x + (p + 1 ) ] = 0 z niewiadomą x .

  • Rozwiąż to równanie dla p = 1 .
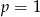  • Wyznacz wszystkie wartości parametru 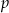p , dla których równanie to ma tylko jedno rozwiązanie.

Rozwiązanie

  • Po wstawieniu 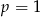p = 1 mamy równanie
    (x + 3)[x2 + 5x + 4] = 0.

    Oczywiście jednym z pierwiastków jest 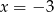x = − 3 , pozostało zająć się trójmianem kwadratowym w nawiasie.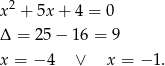

    2 x + 5x + 4 = 0 Δ = 25 − 16 = 9 x = − 4 ∨ x = − 1.

     
    Odpowiedź: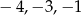 − 4,− 3,− 1

  • Podane równanie ma na pewno jeden pierwiastek 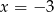x = − 3 . Jeżeli ma to być jedyny pierwiastek, to trójmian kwadratowy w nawiasie musi nie mieć pierwiastków, lub jedynym jego pierwiastkiem musi być 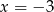x = − 3 . Sprawdźmy kiedy nie ma on pierwiastków (liczymy 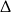Δ -ę).
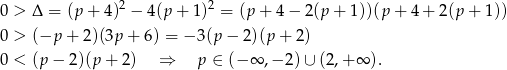
    2 2 0 > Δ = (p + 4) − 4(p + 1) = (p + 4− 2 (p+ 1))(p + 4 + 2(p + 1)) 0 > (−p + 2)(3p + 6) = − 3(p − 2)(p + 2) 0 < (p − 2)(p + 2) ⇒ p ∈ (− ∞ ,− 2)∪ (2 ,+∞ ).

    Pozostało sprawdzić co się dzieje dla p = ± 2 .

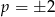    Dla 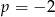p = − 2 , mamy równanie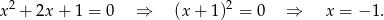

    2 2 x + 2x + 1 = 0 ⇒ (x + 1) = 0 ⇒ x = − 1.

    Zatem wyjściowe równanie ma dwa rozwiązania.

    Dla 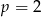p = 2 , mamy równanie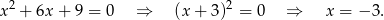

    x 2 + 6x + 9 = 0 ⇒ (x + 3)2 = 0 ⇒ x = − 3.

    Zatem w tym przypadku jest OK.  
    Odpowiedź: p ∈ (− ∞ ,− 2) ∪ ⟨2,+ ∞ )

Wersja PDF