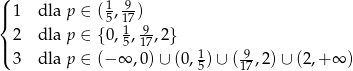/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 6396557

Dodaj do ulubionych
Dodaj do rozwiązanych

Określ liczbę pierwiastków równania 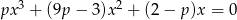3 2 px + (9p − 3)x + (2 − p )x = 0 w zależności od wartości parametru 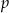p . Naszkicuj wykres funkcji, która każdej wartości parametru 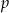p przyporządkowuje liczbę pierwiastków tego równania.

Rozwiązanie

Jeden pierwiastek widać od ręki: 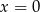x = 0 . Po podzielniu przez x zostaje nam równanie

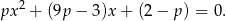
px2 + (9p − 3)x + (2 − p ) = 0.

Jeżeli równanie to jest liniowe, czyli dla 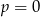p = 0 , to mamy równanie 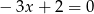− 3x + 2 = 0 , które ma jedno rozwiązanie.

Jeżeli 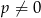p ⁄= 0 to mamy równanie kwadratowe i o ilości jego rozwiązań decyduje znak 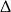Δ -y.

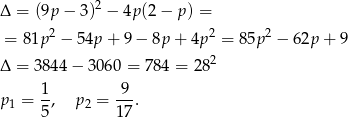
2 Δ = (9p − 3) − 4p (2 − p ) = = 81p 2 − 54p + 9 − 8p + 4p 2 = 85p2 − 62p + 9 2 Δ = 3844 − 30 60 = 784 = 28 1 9 p1 = -, p 2 = ---. 5 17

Mogłoby się wydawać, że to koniec, ale musimy jeszcze sprawdzić kiedy rozwiązaniem jest 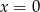x = 0 (żebyśmy nie policzyli go podwójnie).

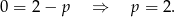
0 = 2 − p ⇒ p = 2.

A zatem ilość rozwiązań równania wyraża się wzorem (pamiętajmy o rozwiązaniu 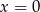x = 0 !)

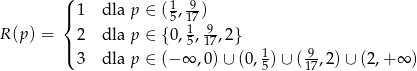
( 1 9- |{ 1 dla p ∈ (5 ,17) R (p) = 2 dla p ∈ { 0, 15,197,2} |( 3 dla p ∈ (− ∞ ,0) ∪ (0, 1) ∪ ( 9-,2)∪ (2 ,+∞ ) 5 17

Teraz bez trudu rysujemy żądany wykres.

PIC

 
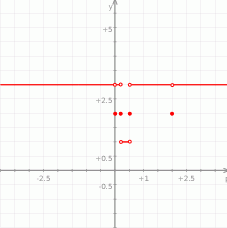
Odpowiedź: ( |{ 1 dla p ∈ (15,197) 2 dla p ∈ {0, 1 , 9-,2} |( 5 17 3 dla p ∈ (− ∞ ,0)∪ (0 , 15)∪ ( 917,2 )∪ (2,+ ∞ )

Wersja PDF