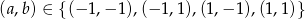Zadanie nr 6630198
Wyznacz wartości parametrów  i
i 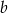 dla których jedynymi rozwiązaniami równania
dla których jedynymi rozwiązaniami równania
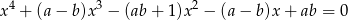
są liczby 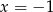 i
i 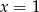 .
.
Rozwiązanie
Sprawdźmy kiedy liczby 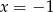 i
i 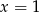 są pierwiastkami danego równania
są pierwiastkami danego równania 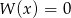 .
.
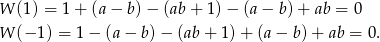
Widzimy więc, że liczby te są zawsze rozwiązaniami tego równania (niezależnie od wartości  i
i 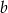 ). Zatem lewa strona równania musi dzielić się przez
). Zatem lewa strona równania musi dzielić się przez
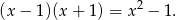
Dzielenie możemy wykonać schematem Hornera, pisemnie lub grupując wyrazy. My jak zwykle wybieramy ostatnią możliwość.
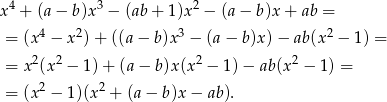
Rozkładamy wielomian kwadratowy w drugim nawiasie.
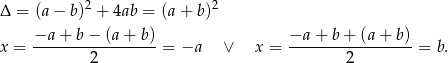
Zatem
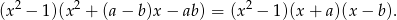
Jeżeli jedynymi pierwiastkami tego wielomianu mają być liczby -1 i 1, to musimy mieć 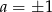 oraz
oraz 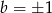 , co daje nam 4 pary rozwiązań
, co daje nam 4 pary rozwiązań
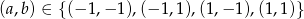
Odpowiedź: