/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 7853557

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że równanie 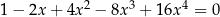2 3 4 1 − 2x + 4x − 8x + 16x = 0 nie ma rozwiązań rzeczywistych.

Rozwiązanie

Sposób I

Spróbujmy tak przekształcić lewą stronę równania, aby występujące tam minusy znalazły się pod kwadratem.

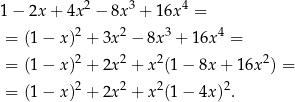
1− 2x+ 4x2 − 8x3 + 16x 4 = 2 2 3 4 = (1− x) + 3x − 8x + 16x = = (1− x)2 + 2x2 + x2(1 − 8x + 16x 2) = 2 2 2 2 = (1− x) + 2x + x (1 − 4x) .

Widać teraz, że jest to suma wyrażeń nieujemnych, które w dodatku nie mogą się jednocześnie zerować. Wyrażenie to jest więc zawsze dodatnie.

Sposób II

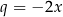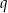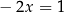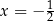Zauważmy, że lewa strona danego równania to suma kolejnych wyrazów ciągu geometrycznego o ilorazie q = − 2x . Możemy ją zatem obliczyć korzystając ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego. Zanim jednak zastosujemy ten wzór, musimy sprawdzić, czy przypadkiem iloraz q nie jest równy 1. Jeżeli jednak − 2x = 1 to x = − 12 i łatwo sprawdzić, że lewa strona równania jest dodatnia.

Możemy zatem założyć, że 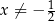1 x ⁄= − 2 i zastosować wzór na sumę kolejnych wyrazów ciągu geometrycznego.

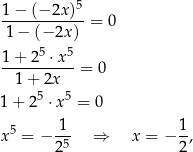
5 1-−-(−-2x)--= 0 1 − (− 2x ) 5 5 1-+-2-⋅-x- = 0 1+ 2x 1+ 25 ⋅x 5 = 0 x5 = − -1- ⇒ x = − 1-, 25 2

co jednak jest sprzeczne z naszym założeniem 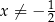1 x ⁄= − 2 . W takim razie podane równanie jest sprzeczne.

Wersja PDF