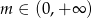Zadanie nr 8124705
Dla jakich wartości parametru 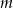 zbiór rozwiązań równania
zbiór rozwiązań równania 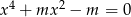 jest dwuelementowy?
jest dwuelementowy?
Rozwiązanie
Równanie jest dwukwadratowe, podstawmy więc 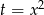 .
.
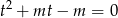
Na początek sprawdźmy kiedy to równanie ma rozwiązania
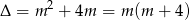
Widać więc, że dla 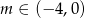 nie w ogóle rozwiązań. Dla
nie w ogóle rozwiązań. Dla 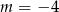 mamy rówanie
mamy rówanie
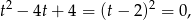
które daje dwa rozwiązania 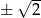 wyjściowego równania.
wyjściowego równania.
Jeżeli 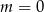 to mamy równanie
to mamy równanie 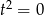 i wyjściowe równanie ma tylko jeden pierwiastek
i wyjściowe równanie ma tylko jeden pierwiastek 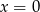 .
.
Pozostała sytuacja, gdy równanie 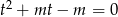 ma dwa różne (i niezerowe) pierwiastki. Zauważmy, że każdy dodatni pierwiastek tego równania daje dwa pierwiastki wyjściowego równania. Zatem równanie to musi mieć jeden pierwiastek ujemny i jeden dodatni (bo ma dwa, a jak ma dwa dodatnie to jest źle). Na mocy wzorów Viète’a iloczyn pierwiastków jest równy
ma dwa różne (i niezerowe) pierwiastki. Zauważmy, że każdy dodatni pierwiastek tego równania daje dwa pierwiastki wyjściowego równania. Zatem równanie to musi mieć jeden pierwiastek ujemny i jeden dodatni (bo ma dwa, a jak ma dwa dodatnie to jest źle). Na mocy wzorów Viète’a iloczyn pierwiastków jest równy 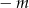 , zatem pierwiastki będą różnych znaków tylko dla
, zatem pierwiastki będą różnych znaków tylko dla 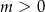 .
.
Łącząc wszystkie rozważone przypadki mamy 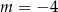 lub
lub 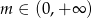 .
.
Odpowiedź: 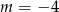 lub
lub