/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 8556164

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie liczby całkowite 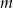m , dla których równanie

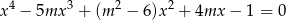
4 3 2 2 x − 5mx + (m − 6)x + 4mx − 1 = 0

nie ma rozwiązań wymiernych.

Rozwiązanie

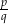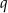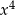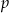Wiemy, że wymierne rozwiązania danego równania muszą być postaci p q , gdzie q dzieli współczynnik przy x4 , a p dzieli wyraz wolny (tu jest ważne, że liczba 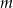m jest liczbą całkowitą, dzięki temu możemy stosować twierdzenie o wymiernych pierwiastkach wielomianów). W naszej sytuacji oznacza to, że pierwiastek wymierny musi być równy 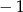− 1 lub 1.

Sprawdźmy kiedy -1 jest pierwiastkiem

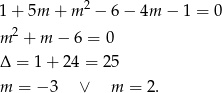
1+ 5m + m 2 − 6 − 4m − 1 = 0 2 m + m − 6 = 0 Δ = 1+ 2 4 = 25 m = − 3 ∨ m = 2.

Teraz sprawdźmy kiedy 1 jest pierwiastkiem

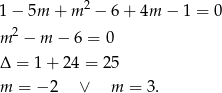
2 1− 5m + m − 6 + 4m − 1 = 0 m 2 − m − 6 = 0 Δ = 1+ 2 4 = 25 m = − 2 ∨ m = 3.

W każdym innym przypadku wielomian nie ma pierwiastków wymiernych.  
Odpowiedź: m ∈ C ∖ {− 3,− 2,2,3}

Wersja PDF