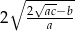/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 8713665

Dodaj do ulubionych
Dodaj do rozwiązanych

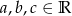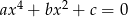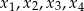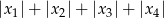Dane są liczby a,b,c ∈ R takie, że równanie 4 2 ax + bx + c = 0 ma cztery rozwiązania rzeczywiste x1,x2,x3,x4 . Oblicz wartość wyrażenia |x1|+ |x 2|+ |x3|+ |x4| .

Rozwiązanie

Dane równanie to równanie dwukwadratowe, które rozwiązujemy podstawiając 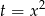t = x 2 . Otrzymujemy wtedy równanie kwadratowe

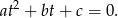
at2 + bt + c = 0 .

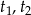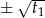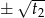Jeżeli dane równanie ma cztery rozwiązania, to powyższe równanie kwadratowe musi mieć dwa rozwiązania dodatnie t1,t2 i wtedy rozwiązaniami wyjściowego równania są liczby -- ± √ t1 i -- ± √ t2 . Interesująca nas suma jest więc równa

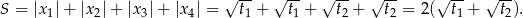
√ -- √ -- √ -- √ -- √ -- √ -- S = |x 1|+ |x2|+ |x 3| + |x4| = t1 + t1 + t2 + t2 = 2( t1 + t2).

Spróbujemy przekształcić powyższe wyrażenie tak, aby móc skorzystać ze wzorów Viète’a.

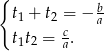
{ t1 + t2 = − b c a t1t2 = a.

Sposób I

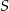S jako suma pierwiastków jest liczbą dodatnią, więc zamiast 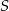S wystarczy obliczyć S 2 .

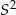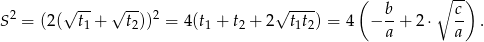
( ∘ -) 2 √ -- √ -- 2 √ ---- b- c- S = (2( t1 + t2)) = 4(t1 + t2 + 2 t1t2) = 4 − a + 2⋅ a .

Zatem

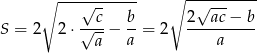
∘ ---√------- ∘ -√-------- ---c b- 2--ac-−-b- S = 2 2 ⋅√ --− a = 2 a a

Sposób II

Liczymy

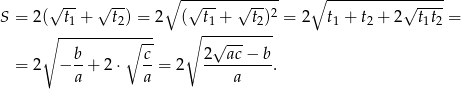
∘ -------------- ∘ ---------------- √ -- √ -- √ -- √ --2 √ ---- S = 2( t1 + t2) = 2 ( t1 + t2) = 2 t1 + t2 + 2 t1t2 = ∘ ---------∘---- ∘ -√-------- b- c- 2--ac-−-b- = 2 − a + 2⋅ a = 2 a .

 
Odpowiedź: ∘ -√----- 2 2-ac−b- a

Wersja PDF