/Szkoła średnia/Równania/Wielomianowe

Zadanie nr 9428797

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 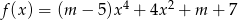4 2 f(x ) = (m − 5 )x + 4x + m + 7 , gdzie 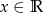x ∈ R . Wyznacz wszystkie wartości parametru 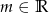m ∈ R , dla których funkcja ma 4 różne miejsca zerowe.

Rozwiązanie

Dana funkcja to funkcja dwukwadratowa, więc możemy podstawić 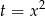t = x 2 .

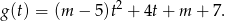
g(t) = (m − 5 )t2 + 4t + m + 7.

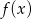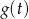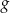Funkcja f (x) będzie miała dwa pierwiastki wtedy i tylko wtedy, gdy funkcja g (t) będzie miała dwa pierwiastki dodatnie (każdy z niech da dwa x -y). Aby tak było, funkcja g musi być kwadratowa, czyli 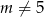m ⁄= 5 . Funkcja 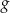g ma dwa pierwiastki, gdy

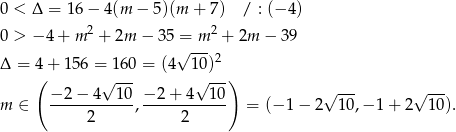
0 < Δ = 16 − 4(m − 5)(m + 7) / : (− 4) 0 > − 4 + m 2 + 2m − 35 = m 2 + 2m − 39 √ ---2 Δ = 4+ 156 = 160 = (4 10) ( √ --- √ ---) √ --- √ --- m ∈ −-2−--4--10, −-2-+-4-1-0 = (− 1− 2 10,− 1 + 2 10 ). 2 2

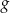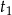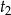Przy tym założeniu funkcja g ma dwa pierwiastki t1 i t2 , które na mocy wzorów Vi’ete‘a spełniają

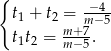
{ t1 + t2 = −m−45 t t = m+-7. 1 2 m− 5

Pierwiastki będą dodatnie jeżeli

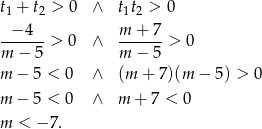
t1 + t2 > 0 ∧ t1t2 > 0 --−-4- m--+-7 m − 5 > 0 ∧ m − 5 > 0 m − 5 < 0 ∧ (m + 7)(m − 5 ) > 0 m − 5 < 0 ∧ m + 7 < 0 m < − 7.

W połączeniu z wcześniej otrzymanymi warunkami otrzymujemy stąd

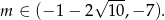
√ --- m ∈ (− 1 − 2 1 0,− 7).

 
Odpowiedź: √ --- m ∈ (− 1− 2 10,− 7)

Wersja PDF