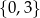Zadanie nr 9767329
Miejscem zerowym wielomianu 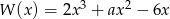 jest liczba
jest liczba 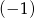 .
.
- Oblicz
 .
. - Wyznacz pozostałe miejsca zerowe
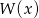 .
.
Rozwiązanie
- Jeżeli
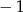 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 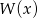 , to
, to 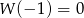 . Liczymy
. Liczymy 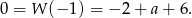
Stąd
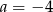 .
.
Odpowiedź: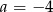
- Liczymy
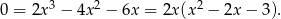
Jednym z pierwiastków jest więc
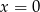 , a pozostałe wyznaczymy rozkładając trójmian w nawiasie.
, a pozostałe wyznaczymy rozkładając trójmian w nawiasie. 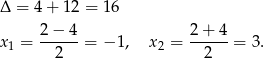
Mogliśmy też drugi pierwiastek wyznaczyć ze wzorów Viète’a: wiemy że jeden jest równy
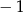 , a iloczyn jest równy
, a iloczyn jest równy 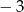 , więc drugi musi być równy 3.
, więc drugi musi być równy 3.
Odpowiedź: