Zadanie nr 3142941
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego do sześciu. Niech 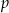 oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy
A) 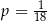 B)
B) 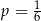 C)
C) 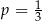 D)
D) 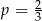
Rozwiązanie
Wyniki rzutów będziemy zapisywać jako pary 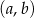 , gdzie
, gdzie  jest wynikiem na pierwszej kostce, a
jest wynikiem na pierwszej kostce, a 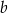 wynikiem na drugiej. Najpierw obliczamy ile jest zdarzeń elementarnych
wynikiem na drugiej. Najpierw obliczamy ile jest zdarzeń elementarnych
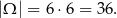
Sposób I
Obliczmy ile jest zdarzeń sprzyjających. W takich zdarzeniach na pierwszej kostce może być dowolna liczba, a drugiej kostce musi być 3 lub 6. W sumie jest więc
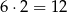
zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest równe
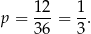
Sposób II
Wypiszmy zdarzenia sprzyjające
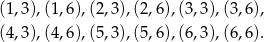
Zatem prawdopodobieństwo wynosi
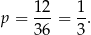
Odpowiedź: C

