Zadanie nr 6749912
W pokoju w kilkunastu ponumerowanych workach znajdują się kolorowe piłki. Miłosz z zamkniętymi oczami wybiera losowo jeden z tych worków, a potem z wybranego worka wybiera jedną piłkę. Prawdopodobieństwo wybrania białej piłki z worka numer 1 jest równe 0,3, a prawdopodobieństwo, że Miłosz wybierze worek numer 1 jest równe 0,4. Jakie jest prawdopodobieństwo tego, że Miłosz wybierze worek numer 1 i z tego worka wyjmie piłkę, która nie jest biała?
A) 0,7 B) 0,9 C) 0,12 D) 0,28
Rozwiązanie
Sposób I
Szkicujemy drzewko opisujące przebieg losowania piłki.
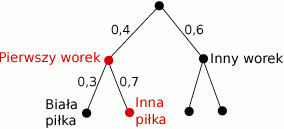
Odczytujemy teraz prawdopodobieństwo interesującego nas zdarzenia (czerwona kropka).
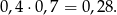
Sposób II
Jeżeli oznaczymy przez 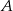 zdarzenie polegające na wylosowaniu białej piłki przez Miłosza, a przez
zdarzenie polegające na wylosowaniu białej piłki przez Miłosza, a przez 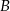 zdarzenie polegające na wybraniu worka numer 1, to wiemy, że
zdarzenie polegające na wybraniu worka numer 1, to wiemy, że
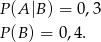
Mamy stąd
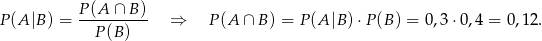
Interesujące nas zdarzenie, tzn. wylosowanie pierwszego worka, z potem wyjęcie z niego piłki, która nie jest biała, to 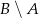 . Mamy zatem
. Mamy zatem
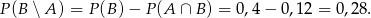
Odpowiedź: D

