Zadanie nr 9182749
Z pudełka zwierającego losy wygrywające i przegrywające wybieramy dwa losy. Prawdopodobieństwo wylosowania co najmniej jednego losu wygrywającego jest równe 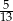 , a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe
, a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe 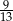 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
A) 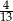 B)
B) 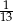 C)
C) 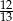 D)
D) 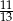
Rozwiązanie
Jeżeli oznaczymy przez 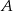 prawdopodobieństwo wylosowania co najmniej jednego losu wygrywającego, a przez
prawdopodobieństwo wylosowania co najmniej jednego losu wygrywającego, a przez 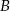 prawdopodobieństwo wylosowania co najwyżej jednego losu wygrywającego, to suma tych zdarzeń zawiera wszystkie możliwe wyniki (bo zawsze jest albo co najmniej jeden, albo co najwyżej jeden los wygrywający). W takim razie
prawdopodobieństwo wylosowania co najwyżej jednego losu wygrywającego, to suma tych zdarzeń zawiera wszystkie możliwe wyniki (bo zawsze jest albo co najmniej jeden, albo co najwyżej jeden los wygrywający). W takim razie
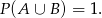
Wiemy ponadto, że 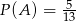 i
i 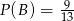 . To, co mamy obliczyć, to
. To, co mamy obliczyć, to 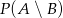 (bo jak jest co najmniej jeden los wygrywający, ale nie jest prawdą, że jest co najwyżej jeden, to są co najmniej dwa).
(bo jak jest co najmniej jeden los wygrywający, ale nie jest prawdą, że jest co najwyżej jeden, to są co najmniej dwa).
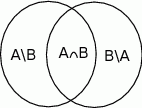
Jeżeli narysujemy diagram Venna to widać, że
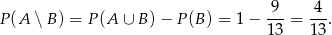
Odpowiedź: A

