/Studia/Analiza/Ciągi/Monotoniczność/Wielomianowe

Zadanie nr 1023144

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj monotoniczność ciągu określonego wzorem 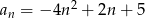2 an = − 4n + 2n + 5 .

Rozwiązanie

Sposób I

Ponieważ przy 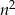2 n mamy ujemny współczynnik, to z własności funkcji kwadratowej, ciąg będzie od pewnego miejsca malejący (myślimy o ciągu jak o funkcji, której argumenty to 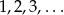1,2,3,... ). Pytanie tylko od którego. Wierzchołek paraboli ma pierwszą współrzędną 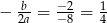− -b = −2-= 1 2a −8 4 , więc od początku ciąg będzie malejący (bo wszystkie argumenty 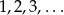1,2,3 ,... leżą na prawo od wierzchołka).

Sposób II

Możemy też zbadać monotoniczność wprost.

Badamy różnicę 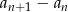an +1 − an (jezeli jest dodatnia to ciąg jest rosnący, jeżeli ujemna to jest malejący). Liczymy

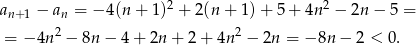
2 2 an +1 − an = − 4(n + 1) + 2(n + 1 )+ 5 + 4n − 2n − 5 = = − 4n2 − 8n − 4 + 2n + 2 + 4n 2 − 2n = − 8n − 2 < 0.

Zatem ciąg jest malejący.  
Odpowiedź: Ciąg jest malejący.

Wersja PDF