Zadanie nr 2990445
Zbadaj monotoniczność ciągu określonego wzorem 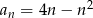 .
.
Rozwiązanie
Liczymy różnicę 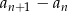 .
.
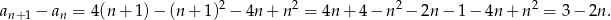
Wyrażenie to jest ujemne o ile 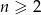 , czyli ciąg jest malejący począwszy od drugiego wyrazu.
, czyli ciąg jest malejący począwszy od drugiego wyrazu.
Odpowiedź: Malejący począwszy od drugiego wyrazu.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Zbadaj monotoniczność ciągu określonego wzorem 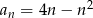 .
.
Liczymy różnicę 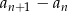 .
.
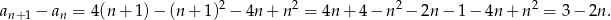
Wyrażenie to jest ujemne o ile 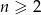 , czyli ciąg jest malejący począwszy od drugiego wyrazu.
, czyli ciąg jest malejący począwszy od drugiego wyrazu.
Odpowiedź: Malejący począwszy od drugiego wyrazu.
