Zadanie nr 1655854
Ciąg 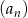 jest rosnący. Co można powiedzieć o monotoniczności ciągu
jest rosnący. Co można powiedzieć o monotoniczności ciągu 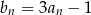 ?
?
Rozwiązanie
Skoro ciąg jest rosnący to
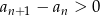
dla 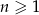 .
.
Liczymy różnicę kolejnych wyrazów ciągu 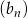 .
.
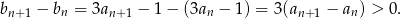
Odpowiedź: Ciąg jest rosnący.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 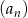 jest rosnący. Co można powiedzieć o monotoniczności ciągu
jest rosnący. Co można powiedzieć o monotoniczności ciągu 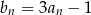 ?
?
Skoro ciąg jest rosnący to
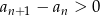
dla 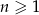 .
.
Liczymy różnicę kolejnych wyrazów ciągu 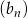 .
.
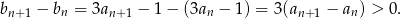
Odpowiedź: Ciąg jest rosnący.
