/Studia/Analiza/Ciągi/Monotoniczność/Różne

Zadanie nr 3936127

Dodaj do ulubionych
Dodaj do rozwiązanych

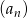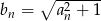Ciąg (an) jest malejący i wszystkie jego wyrazy są dodatnie. Co można powiedzieć o monotoniczność ciągu ∘ ------- bn = a2n + 1 ?

Rozwiązanie

Skoro ciąg jest malejący to

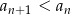
an+ 1 < an

dla 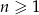n ≥ 1 .
Wyrazy są dodatnie, więc

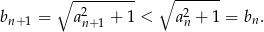
∘ --------- ∘ ------- bn+1 = a2 + 1 < a2 + 1 = bn. n+1 n

Zatem ciąg jest malejący.  
Odpowiedź: Ciąg jest malejący.

Wersja PDF