/Studia/Analiza/Ciągi/Monotoniczność/Z kropkami

Zadanie nr 5462951

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj monotoniczność ciągu 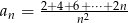2+4+-6+-⋅⋅⋅+-2n an = n2 .

Rozwiązanie

W liczniku mamy sumę n kolejnych wyrazów ciągu arytmetycznego, więc

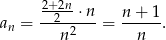
2+-2n a = --2--⋅n- = n-+-1-. n n2 n

Aby sprawdzić monotoniczność ciągu sprawdzamy, czy iloraz kolejnych wyrazów jest mniejszy, czy też większy od 1 (ciąg ma wyrazy dodatnie).

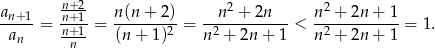
an+ 1 nn++21- n(n + 2) n2 + 2n n 2 + 2n + 1 ----- = -n+1-= -------2-= -2----------< --2--------- = 1. an n (n + 1) n + 2n + 1 n + 2n + 1

Zatem ciąg jest malejący.  
Odpowiedź: Ciąg malejący.

Wersja PDF