Równania wielomianowe stopnia 3

Wszyscy znamy bardzo wygodne wzory na rozwiązania równania kwadratowego. Z drugiej strony wiadomo, że takie wzory nie mogą istnieć dla równań stopnia większego od 4. Znana jest ponadto metoda sprowadzania równań stopnia 4 do równań stopnia 3 (jest ona dość skomplikowana, więc nie wchodzimy w szczegóły). W takiej sytuacji jedyny ciekawy przypadek, to przypadek równania stopnia 3:

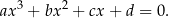
ax 3 + bx 2 + cx+ d = 0.

Wzory w tym przypadku noszą nazwę wzorów Cardano i właśnie im będzie poświęcony ten poradnik.

Podkreślmy, że w wielu sytuacjach są prostsze metody rozwiązywania równań stopnia 3, o czym możecie dokładnie poczytać w poradniku o rozwiązywaniu równań wielomianowych. 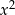x 2 mówimy: pa,pa Postać wzorów Cardano w przypadku napisanego wyżej, ogólnego równania, jest bardzo skomplikowana, dlatego na początku spróbujemy je trochę uprościć.

Po pierwsze możemy równanie podzielić stronami przez , co sprowadza nas do sytuacji ze współczynnikiem równym 1 przy :

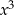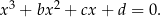
3 2 x + bx + cx + d = 0 .

Kolejny krok to podstawienie 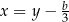b x = y − 3 . Sprawdźmy jak zmieni się równanie po takim podstawieniu.

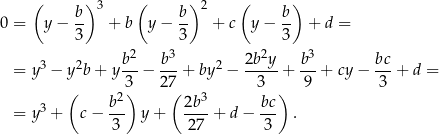
( ) 3 ( )2 ( ) b- b- -b 0 = y− 3 + b y − 3 + c y − 3 + d = 2 3 2 3 = y3 − y2b + yb--− b--+ by2 − 2b--y+ b--+ cy − bc-+ d = 3 27 3 9 3 ( b2) ( 2b3 bc) = y3 + c− --- y + ----+ d − --- . 3 27 3

Wprawdzie współczynniki trochę się nam skomplikowały, ale za to zniknęła niewiadoma w kwadracie, co pozwala nam zajmować się równaniem postaci

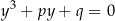
y3 + py + q = 0

(jest to spore uproszczenie, bo zostały nam już tylko dwa parametry).

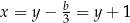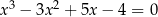Podstawmy b x = y− 3 = y + 1 w równaniu 3 2 x − 3x + 5x − 4 = 0 .
Liczymy

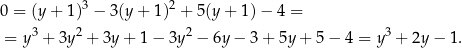
0 = (y + 1 )3 − 3(y + 1 )2 + 5(y + 1 )− 4 = 3 2 2 3 = y + 3y + 3y + 1 − 3y − 6y− 3+ 5y+ 5− 4 = y + 2y − 1.

Widać zatem, że zamieniliśmy wyjściowe równanie na równanie, w którym nie ma 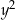2 y .

Wyróżnik Podobnie jak dla równania kwadratowego, deﬁniujemy wyróżnik równania

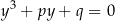
y3 + py + q = 0

wzorem

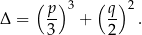
( ) ( ) Δ = p- 3 + q- 2. 3 2

Nie powinno być zaskoczeniem, że znak wyróżnika pozwala stwierdzić ile rozwiązań ma równanie, dokładny opis możliwych sytuacji zrobimy jednak odrobinę później. Wzór Cardano Nie przedłużając, liczba

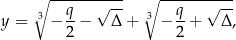
∘ ------√--- ∘ ------√--- y = 3 − q− Δ + 3 − q-+ Δ , 2 2

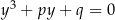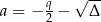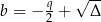jest zawsze pierwiastkiem równania y3 + py + q = 0 . Jest to właśnie wspominany już wzór Cardano. Zanim omówimy dokładnie różne niuanse związane z tym wzorem sprawdźmy, że rzeczywiście jest on poprawny. Żeby ułatwić sobie zapis, oznaczmy q √ -- a = − 2 − Δ i q √ -- b = − 2 + Δ . W szczególności

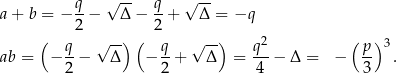
q- √ -- q- √ -- a+ b = − 2 − Δ − 2 + Δ = −q ( √ -) ( √ --) 2 ( )3 ab = − q− Δ − q-+ Δ = q--− Δ = − p- . 2 2 4 3

Teraz już jesteśmy gotowi do rachunków. Sprawdzimy, że 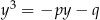3 y = −py − q .

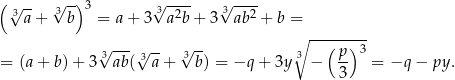
( √ -) 3 √ ---- √ ---- √3a--+ 3b = a+ 3 3a2b + 3 3ab2 + b = ∘ -------- √3 ---√ -- 3√ -- 3 ( p) 3 = (a+ b )+ 3 ab( 3 a+ b) = −q + 3y − -- = −q − py . 3

Czyli wszystko cacy. Znak wyróżnika

Jeżeli 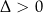to równanie 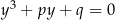ma dokładnie jeden pierwiastek i jest on równy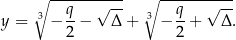

$∘ --q---√--- ∘ --q---√--- y = 3 − -− Δ + 3 − --+ Δ . 2 2$

Rozwiążmy równanie .
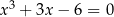Liczymy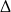 -ę.

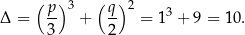
$( ) ( ) Δ = p- 3 + q- 2 = 13 + 9 = 10. 3 2$

Zatem jest jeden pierwiastek i jest on równy

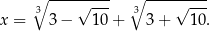
$∘ ----√---- ∘ ----√---- x = 3 3 − 10 + 3 3+ 10.$

Rozwiążmy równanie .
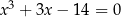Liczymy dokładnie tak samo jak poprzednio.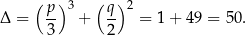

$(p-)3 ( q) 2 Δ = 3 + 2 = 1+ 49 = 50.$

Zatem jedyny pierwiastek jest równy

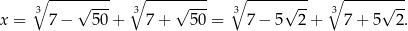
$∘ --------- ∘ --------- ∘ --------- ∘ --------- 3 √ --- 3 √ --- 3 √ -- 3 √ -- x = 7− 50+ 7 + 50 = 7− 5 2 + 7 + 5 2 .$

Zaraz, zaraz, przecież pierwiastek wyjściowego równania można łatwo zgadnąć bez wzorów Cardano: jest to 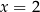! Nie jest to żadna sprzeczność, po prostu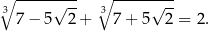

$∘ --------- ∘ --------- 3 √ -- 3 √ -- 7− 5 2 + 7 + 5 2 = 2.$

Powinno być teraz dla was jasne skąd biorą się zadania takie jak to.
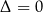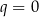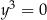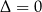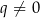Jeżeli i to mamy równanie , które ma jeden pierwiastek potrójny. Jeżeli natomiast i to równanie ma dwa różne pierwiastki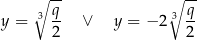

$∘ -q ∘ q- y = 3 -- ∨ y = − 2 3 -- 2 2$

i jeden z nich jest podwójny.
Rozwiążmy równanie .
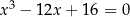Liczymy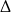 -ę.

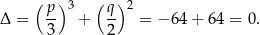
$( ) ( ) p- 3 q- 2 Δ = 3 + 2 = − 64+ 64 = 0.$

Zatem równanie ma dwa rozwiązania

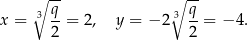
$∘ -- ∘ -- 3 q 3 q x = --= 2 , y = − 2 --= − 4. 2 2$

Można sprawdzić, że 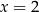jest pierwiastkiem podwójnym, czyli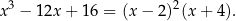

$3 2 x − 12x + 16 = (x − 2 ) (x+ 4).$
No i została nam najciekawsza sytuacja, gdy 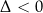. Równanie ma wtedy trzy pierwiastki. Są różne triki, żeby w tym miejscu udawać, że można się obejść bez liczb zespolonych, ale my jak zwykle staramy się pisać jak jest naprawdę, a prawda jest taka, że właśnie znaleźliśmy się w historycznej sytuacji, w której ludzie zdali sobie sprawę, że „nie da się żyć” bez pierwiastków kwadratowych z liczb ujemnych. Sytuację tę omówimy w następnym rozdziale.

Casus irreducibilis Idea jest taka: wiemy, że równanie ma trzy pierwiastki rzeczywiste, więc wystarczy znać jeden z nich i dalej już poradzimy sobie jak w szkole, dzieląc przez dwumian itd. Jak zatem znaleźć jeden pierwiastek? Jest nim dokładnie pierwiastek ze wzoru Cardano, czyli liczba

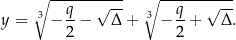
---------- ---------- ∘ q √ -- ∘ q √ -- y = 3 − -− Δ + 3 − --+ Δ . 2 2

Przypomnijmy, że sprawdziliśmy (nie przejmując się 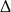-ą), że po wstawieniu tej liczby do równości 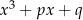x 3 + px + q otrzymujemy 0.

No i fajnie, więc jaki jest problem? Problem jest taki, że jesteśmy w przypadku 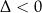Δ < 0 , więc w powyższym wyrażeniu mamy dwa razy pierwiastek kwadratowy z liczby ujemnej 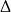! Oczywiście od początku się to ludziom (matematykom) nie podobało, więc bardzo się starali jakoś ten wzór zapisać tak, aby nie było tych dziwnych pierwiastków. Okazuje się jednak, że nie da się tego zrobić. Co gorsza wiemy, że pierwiastki równania są liczbami rzeczywistymi, więc to dziwaczne wyrażenie jest tak naprawdę „magicznym” zapisem zwykłej liczby rzeczywistej.

Rozwiążmy równanie 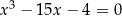3 x − 15x − 4 = 0 .
Mamy

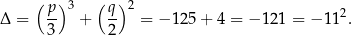
(p )3 ( q)2 Δ = -- + -- = − 1 25+ 4 = − 121 = − 1 12. 3 2

Zatem jeden z pierwiastków równania jest równy

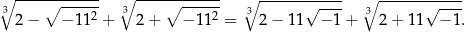
3∘ ----∘------- ∘3 ----∘------- ∘3 ------√----- ∘3------√------ 2 − − 1 12 + 2+ − 112 = 2− 11 − 1 + 2 + 11 −1 .

Liczba ta oczywiście wygląda podejrzanie, ale przykład ten jest tak dobrany, że możemy bezpośrednio sprawdzić, że jest to tak naprawdę liczba rzeczywista: wyrażenia pod oboma pierwiastkami są pełnymi sześcianami.

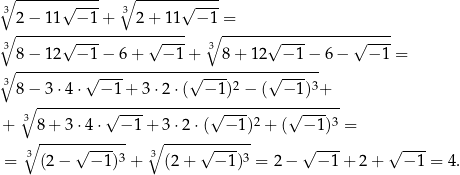
∘3 ------√----- 3∘ ------√----- 2− 11 − 1+ 2 + 11 − 1 = ∘ ------√-----------√----- ∘ ------√-----------√----- 3 8− 12 − 1− 6+ − 1+ 3 8+ 12 − 1 − 6 − − 1 = ∘ ---------√-------------√----------√------- 3 8− 3⋅4 ⋅ − 1 + 3⋅ 2⋅( − 1)2 − ( − 1)3+ ∘ ------------------------------------------ + 38 + 3 ⋅4 ⋅√ −-1+ 3⋅2 ⋅(√ −-1)2 + (√ −-1)3 = ∘ ------------ ∘ ------------ 3 √ ----3 3 √ ----3 √ ---- √ ---- = (2− − 1) + (2+ − 1) = 2 − − 1+ 2+ − 1 = 4.

Nie było łatwo, ale widać, że wzory Cardano dały nam po prostu bardzo oryginalny sposób na zapisanie liczby 4. Łatwo sprawdzić, że 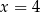x = 4 jest rzeczywiście pierwiastkiem oryginalnego równania.
Powyższe przekształcenie nie powinno nas dziwić, widzieliśmy już w przypadku 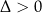Δ > 0 , że wzory Cardano potraﬁą prostą liczbę zapisać w skomplikowany sposób.

Jeżeli lekko zmodyﬁkujemy poprzedni przykład: 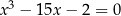3 x − 15x − 2 = 0 to mamy

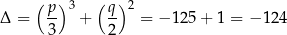
( p) 3 ( q) 2 Δ = -- + -- = − 125 + 1 = − 12 4 3 2

i jeden z pierwiastków jest równy

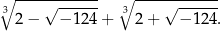
∘ ------------ ∘ ------------ 3 2 − √ −-124-+ 32 + √ −-12-4.

Teraz jednak nie ma już łatwego sposobu na pozbycie się pierwiastków z liczb ujemnych i mamy w takiej sytuacji dwa wyjścia:

albo jesteśmy konserwatywni i uważamy, że pierwiastki z liczb ujemnych nie mają sensu; w tym przypadku musimy się pogodzić z faktem, że nie umiemy rozwiązać równania 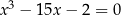(bo uważamy powyższy wzór za bezsensowny);
albo jesteśmy postępowi i uaktualniamy nasze pojęcie liczby tak, aby powyższy wzór był OK; w ten sposób odkrywamy świat liczb zespolonych.

Oczywiście matematycy obrali drugą drogę (w XVI wieku).

Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Funkcje/Wielomiany/Stopnia 3