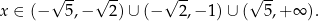Najprostsze nierówności wielomianowe to nierówności liniowe i kwadratowe. Ponieważ jednak omówiliśmy je w osobnych poradnikach, skupimy się teraz wyłącznie na nierównościach stopnia co najmniej 3. Proste nierówności Do rozwiązania prostych nierówności wielomianowych na ogół wystarcza odrobina zdrowego rozsądku.
Rozwiążmy nierówność 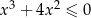 .
.
Rozkładamy lewą stronę
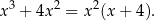
Wyrażenie 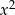 jest dodatnie o ile
jest dodatnie o ile 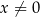 . Pamiętamy zatem o dołożeniu na końcu
. Pamiętamy zatem o dołożeniu na końcu 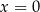 do zbioru rozwiązań i możemy nie zwracać uwagi na
do zbioru rozwiązań i możemy nie zwracać uwagi na 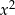 (lub jak ktoś woli dzielimy nierówność stronami przez
(lub jak ktoś woli dzielimy nierówność stronami przez 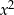 ). Pozostaje nam więc nierówność
). Pozostaje nam więc nierówność
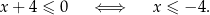
Zatem rozwiązaniem jest zbiór 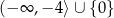 .
.
Rozwiążmy nierówność 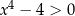 .
.
Rozkładamy lewą stronę.
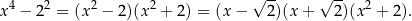
Ostatni składnik jest dodatni, więc zostaje nam nierówność kwadratowa
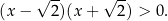
Zatem 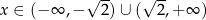 .
.
Rozwiążmy nierówność 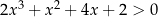 .
.
Zauważmy, że dwa ostatnie współczynniki: 4 i 2 to wielokrotności pierwszych dwóch współczynników: 2 i 1. Taka sytuacja to typowy znak, że możemy coś wyłączyć przed nawias.
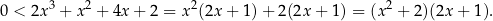
Mamy zatem 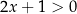 , czyli
, czyli 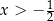 .
.
Nierówności stopnia 3 Zanim powiemy jak rozwiązywać dowolną nierówność wielomianową, prześledźmy przypadek nierówności stopnia 3. Jest to najczęściej spotykana sytuacja w zadaniach szkolnych, a ponadto jest to dobre wprowadzenie do ogólnej metody, o której powiemy w dalszej części.
Wielomian stopnia 3 ma zawsze co najmniej jeden pierwiastek, więc po lekturze poradnika o dzieleniu wielomianów, powinniśmy już umieć go rozłożyć na iloczyn dwumianu 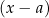 oraz trójmianu kwadratowego. Żeby nie komplikować sytuacji, powiedzmy, że mamy do rozwiązania nierówność
oraz trójmianu kwadratowego. Żeby nie komplikować sytuacji, powiedzmy, że mamy do rozwiązania nierówność
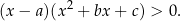
Mamy teraz dwie możliwości.
-
Jeżeli trójmian
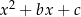 jest zawsze dodatni (czyli
jest zawsze dodatni (czyli 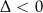 ), to pozostaje nam nierówność
), to pozostaje nam nierówność 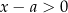 , czyli rozwiązaniem jest zbiór
, czyli rozwiązaniem jest zbiór 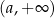 .
. -
W przeciwnym przypadku, trójmian w nawiasie możemy rozłożyć na czynniki liniowe i dostajemy nierówność
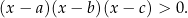
Jeżeli teraz dwie z tych liczb są równe, np.
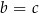 to mamy czynnik
to mamy czynnik 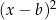 , który możemy pominąć, o ile tylko
, który możemy pominąć, o ile tylko 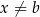 (bo wtedy jest on dodatni). Zatem pozostaje nam nierówność
(bo wtedy jest on dodatni). Zatem pozostaje nam nierówność 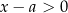 , czyli
, czyli 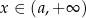 . Na koniec trzeba pamiętać o wyrzuceniu
. Na koniec trzeba pamiętać o wyrzuceniu 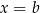 ze zbioru rozwiązań (jeżeli w nim jest).
ze zbioru rozwiązań (jeżeli w nim jest). Jeżeli natomiast żadne dwie spośród liczb
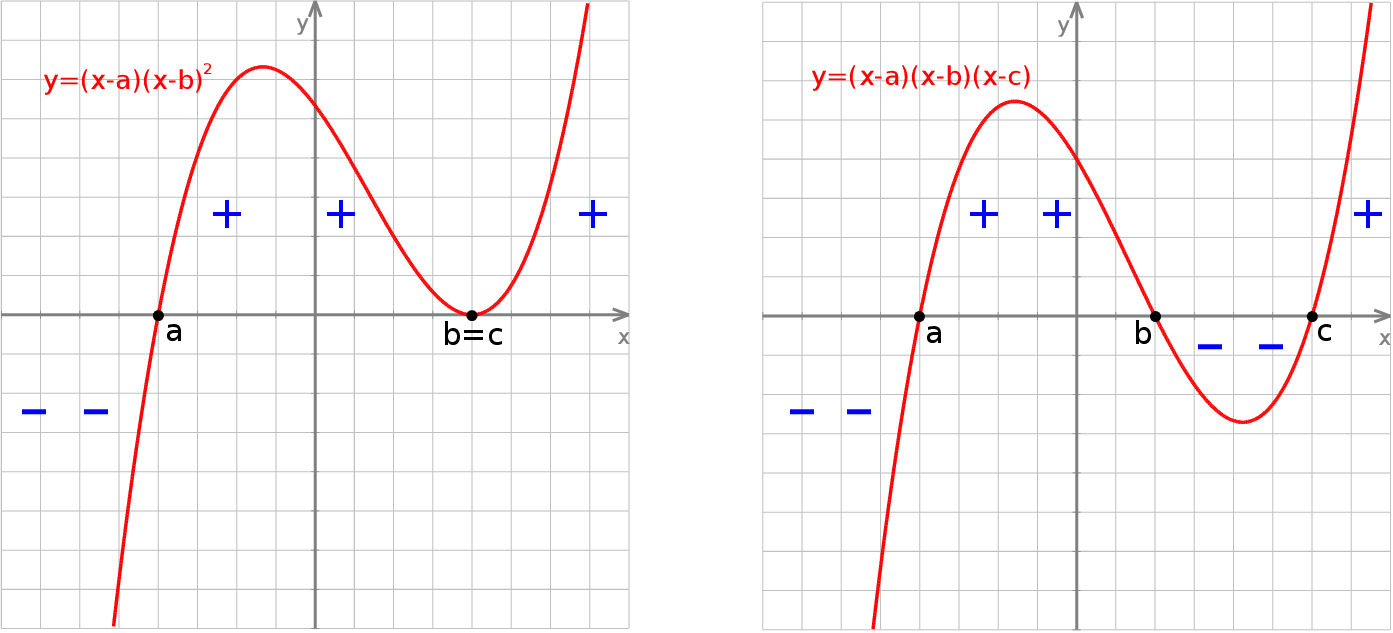
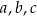 nie są równe, powiedzmy, że
nie są równe, powiedzmy, że 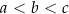 to szkicujemy wykres wielomianu
to szkicujemy wykres wielomianu 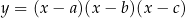 i z wykresu odczytujemy rozwiązanie:
i z wykresu odczytujemy rozwiązanie: 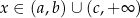 .
. 
Oczywiście opisana przez nas sytuacja nierówności postaci
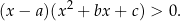
nie wyczerpuje wszystkich możliwości (np. słabych nierówności), ale powinno być jasne, że sam schemat się nie zmienia.
Rozwiążmy nierówność 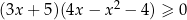 .
.
W drugim nawiasie mamy wzór skróconego mnożenia, czyli
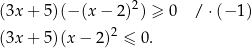
Oczywiście dla 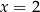 jest OK, a dla
jest OK, a dla 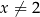 drugi nawias jest dodatni, więc pozostaje nierówność
drugi nawias jest dodatni, więc pozostaje nierówność

zatem rozwiązaniem jest zbiór 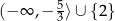 .
.
Rozwiążmy nierówność 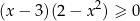 .
.
Przekształcamy
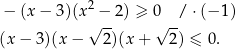
Mając teraz w pamięci wykres funkcji postaci 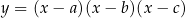 (obrazek powyżej) odczytujemy rozwiązanie
(obrazek powyżej) odczytujemy rozwiązanie
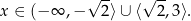
Metoda węża Widzieliśmy już kilka przykładów nierówności wielomianowych, więc możemy w końcu przejść do sytuacji ogólnej. Schemat postępowania w tym przypadku rozbijemy na 3 kroki.
1. Pierwszy krok przypomina rozwiązywanie równań wielomianowych: rozkładamy dany wielomian na czynniki liniowe i kwadratowe, które nie mają pierwiastków. Czynniki kwadratowe bez pierwiastków w zasadzie nas nie interesują, bo są albo zawsze dodatnie (więc możemy je pominąć), albo zawsze ujemne (możemy je pominąć zmieniając znak nierówności na przeciwny). Możemy też założyć, że czynniki liniowe są postaci 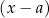 , a nie np.
, a nie np. 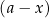 (jeżeli tak nie jest to zamieniamy każde
(jeżeli tak nie jest to zamieniamy każde 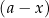 na
na 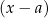 zmieniając znak nierówności na przeciwny). Tak więc po wykonaniu tego kroku możemy założyć, że nasz wielomian jest iloczynem czynników liniowych postaci
zmieniając znak nierówności na przeciwny). Tak więc po wykonaniu tego kroku możemy założyć, że nasz wielomian jest iloczynem czynników liniowych postaci 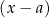 .
.
W nierówności 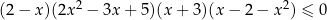 drugi nawias jest zawsze dodatni, a czwarty zawsze ujemny, więc nierówność jest równoważna nierówności postaci
drugi nawias jest zawsze dodatni, a czwarty zawsze ujemny, więc nierówność jest równoważna nierówności postaci
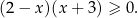
Jeżeli dodatkowo zamienimy kolejność składników w pierwszym nawiasie to mamy nierówność
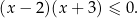
2. Może się zdarzyć, że w otrzymanym rozkładzie niektóre czynniki się powtarzają. Jest na to prosta rada: składniki postaci 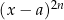 są zawsze nieujemne, więc możemy je pominąć, pamiętając tylko o dołączeniu (wyrzuceniu)
są zawsze nieujemne, więc możemy je pominąć, pamiętając tylko o dołączeniu (wyrzuceniu) 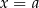 do (ze) zbioru rozwiązań w przypadku słabej (ostrej) nierówności. Po wykonaniu tego kroku pozostanie nam wielomian postaci
do (ze) zbioru rozwiązań w przypadku słabej (ostrej) nierówności. Po wykonaniu tego kroku pozostanie nam wielomian postaci 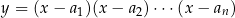 , gdzie każde dwie spośród liczb
, gdzie każde dwie spośród liczb 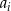 są różne.
są różne.
W nierówności 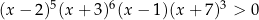 możemy pominąć (tzn. podzielić przez nie nierówność stronami) czynniki
możemy pominąć (tzn. podzielić przez nie nierówność stronami) czynniki 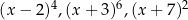 . Pozostanie nam zatem nierówność
. Pozostanie nam zatem nierówność
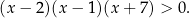
Przekształcenie to ma sens, o ile tylko będziemy pamiętać o wyrzuceniu liczb 2,-3,-7 ze zbioru rozwiązań.
W nierówności 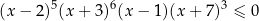 możemy pominąć (tzn. podzielić przez nie nierówność stronami) czynniki
możemy pominąć (tzn. podzielić przez nie nierówność stronami) czynniki 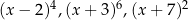 . Pozostanie nam zatem nierówność
. Pozostanie nam zatem nierówność
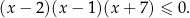
Przekształcenie to ma sens, o ile tylko będziemy pamiętać o dodaniu liczb 2,-3,-7 do zbioru rozwiązań.
3. Po wykonaniu poprzednich dwóch kroków pozostała nam nierówność, w której wielomian ma postać
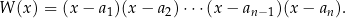
Możemy dodatkowo założyć (zmieniając ewentualnie kolejność nawiasów), że
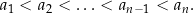
Teraz nadeszła pora na tytułowego węża: rysujemy oś liczbową i zaznaczamy na niej liczby 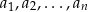 w kolejności od najmniejszej do największej (rysunek ma być schematyczny, odległości między liczbami nie mają żadnego znaczenia, ważna jest tylko ich prawidłowa kolejność na osi).
w kolejności od najmniejszej do największej (rysunek ma być schematyczny, odległości między liczbami nie mają żadnego znaczenia, ważna jest tylko ich prawidłowa kolejność na osi).

Następnie, startując od prawej strony, ciągniemy przez zaznaczone punkty węża, który jest na przemian powyżej i poniżej osi. Pamiętajmy, że startujemy zawsze z prawej strony i powyżej osi. Z tego obrazka odczytujemy rozwiązanie intersującej nas nierówności: fragmenty węża, które są powyżej osi odpowiadają przedziałom, na których 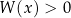 , a fragmenty poniżej osi przedziałom, na których
, a fragmenty poniżej osi przedziałom, na których 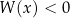 (jeżeli interesuje nas słaba nierówność, to po prostu dołączamy końce przedziałów). Na zakończenie należy uwzględnić ewentualne korekty rozwiązania wynikające z 2. punktu algorytmu (odpowiadające pierwiastkom wielokrotnym).
(jeżeli interesuje nas słaba nierówność, to po prostu dołączamy końce przedziałów). Na zakończenie należy uwzględnić ewentualne korekty rozwiązania wynikające z 2. punktu algorytmu (odpowiadające pierwiastkom wielokrotnym).
Rozwiążmy nierówność
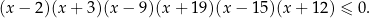
Rysujemy węża przez pierwiastki lewej strony.

Z węża odczytujemy rozwiązanie
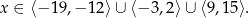
Rozwiążmy nierówność 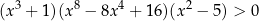 .
.
Rozpoczynamy od rozłożenia lewej strony na czynniki.
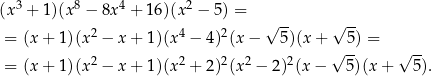
Drugi i trzeci nawias są zawsze dodatnie, a czwarty jest dodatni o ile tylko 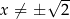 . Pamiętamy zatem o wyrzuceniu
. Pamiętamy zatem o wyrzuceniu 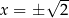 ze zbioru rozwiązań i otrzymujemy nierówność
ze zbioru rozwiązań i otrzymujemy nierówność
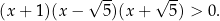
Z węża łatwo odczytać, że 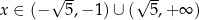 .
.

Musimy jeszcze wyrzucić z tego zbioru 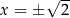 i otrzymujemy rozwiązanie
i otrzymujemy rozwiązanie