Zadanie nr 6416603
Korzystając z definicji funkcji rożnowartościowej wykaż, że funkcja 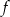 określona wzorem
określona wzorem 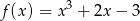 jest rożnowartościowa.
jest rożnowartościowa.
Rozwiązanie
Musimy wykazać, że jeżeli 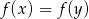 to
to 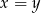 . Liczymy
. Liczymy
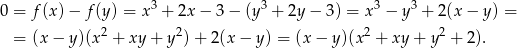
Jeżeli uda nam się wykazać, że wyrażenie w drugim z nawiasów jest niezerowe, to będzie koniec, bo powyższa równość będzie oznaczać, że 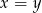 . Przekształćmy (zwiniemy do pełnego kwadratu)
. Przekształćmy (zwiniemy do pełnego kwadratu)
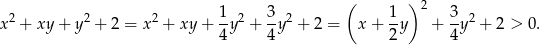
Wyrażenie to jest więc niezerowe, co oznacza, że 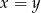 .
.

