/Szkoła średnia/Funkcje/Wielomiany/Stopnia 3

Zadanie nr 8791571

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 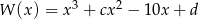3 2 W (x) = x + cx − 10x + d jest podzielny przez dwumian 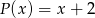P (x) = x + 2 . Przy dzieleniu wielomianu 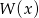W (x) przez dwumian 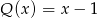Q (x) = x− 1 otrzymujemy resztę 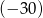(− 30) . Oblicz pierwiastki wielomianu 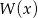W (x ) i rozwiąż nierówność W (x) ≥ 0 .

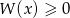Rozwiązanie

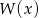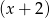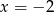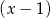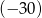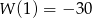Jeżeli wielomian W (x) jest podzielny przez dwumian (x + 2) , to x = − 2 musi być jego pierwiastkiem. Podobnie, jeżeli reszta z dzielenia przez dwumian (x− 1) jest równa (− 30 ) , to W (1) = − 30 . Mamy zatem układ równań

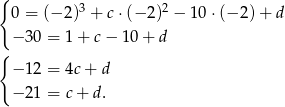
{ 0 = (− 2 )3 + c ⋅(− 2)2 − 10⋅ (− 2 )+ d − 30 = 1+ c − 10 + d { − 12 = 4c+ d − 21 = c+ d .

Odejmujemy teraz od pierwszego równania drugie i mamy

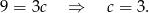
9 = 3c ⇒ c = 3 .

Stąd 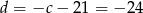d = −c − 21 = − 24 i

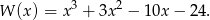
W (x) = x3 + 3x 2 − 10x − 24.

Wiemy już, że jednym z pierwiastków jest 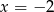x = − 2 , więc dzielimy ten wielomian przez 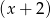(x+ 2) – my zrobimy to grupując wyrazy.

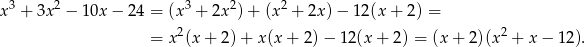
3 2 3 2 2 x + 3x − 10x − 24 = (x + 2x ) + (x + 2x) − 12(x + 2 ) = = x2(x + 2) + x(x + 2) − 12(x + 2) = (x + 2)(x2 + x − 12).

Szukamy teraz pierwiastków trójmianu w drugim nawiasie.

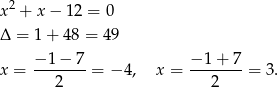
2 x + x − 12 = 0 Δ = 1+ 48 = 49 −1 − 7 − 1+ 7 x = -------= − 4, x = ------- = 3. 2 2

Zatem

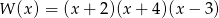
W (x) = (x+ 2)(x+ 4)(x − 3)

i rozwiązaniem nierówności 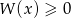W (x ) ≥ 0 jest zbiór

⟨− 4,− 2⟩∪ ⟨3,+ ∞ ) .

 
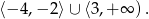
Odpowiedź: 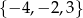{− 4,− 2,3} , ⟨− 4,− 2⟩ ∪ ⟨3,+ ∞ )

Wersja PDF