Zadanie nr 8558100
Funkcje 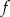 i
i 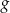 są określone dla wszystkich liczb rzeczywistych
są określone dla wszystkich liczb rzeczywistych 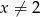 wzorami:
wzorami: 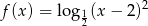 ,
, 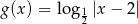 . Ile punktów wspólnych mają wykresy tych funkcji?
. Ile punktów wspólnych mają wykresy tych funkcji?
A) 0 B) 1 C) 2 D) 4
Rozwiązanie
Musimy ustalić, ile miejsc zerowych ma funkcja
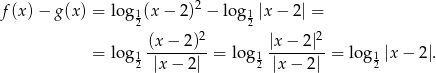
Sposób I
Szkicujemy wykres funkcji 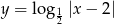 . Jest to wykres funkcji
. Jest to wykres funkcji 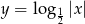 przesunięty o dwie jednostki w prawo, a wykres
przesunięty o dwie jednostki w prawo, a wykres 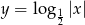 , to dwie kopie wykresu
, to dwie kopie wykresu 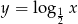 umieszczone symetrycznie względem osi
umieszczone symetrycznie względem osi 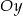 .
.
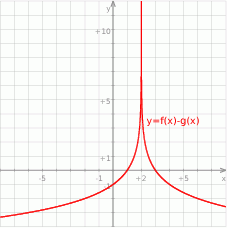
Z rysunku widać, że funkcja 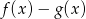 ma dwa miejsca zerowe.
ma dwa miejsca zerowe.
Sposób II
Rozwiązujemy równanie
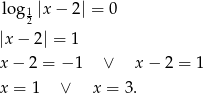
Sposób III
Szukamy punktów wspólnych wykresów funkcji 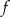 i
i 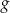 .
.
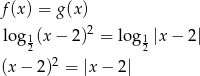
Jeżeli 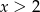 to mamy stąd
to mamy stąd

a jeżeli 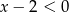 , to mamy
, to mamy

Odpowiedź: C

