Zadanie nr 6129547
Oblicz całkę 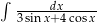 .
.
Rozwiązanie
Stosujemy podstawienie uniwersalne 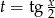 .
.
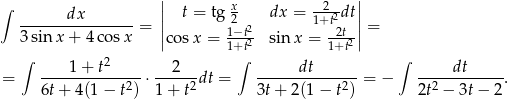
Ostatnią całkę obliczamy korzystając z rozkładu na ułamki proste.
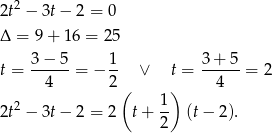
Szukamy więc rozkładu postaci
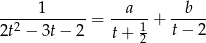
Mnożąc stronami przez 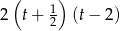 mamy
mamy
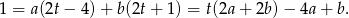
Mamy zatem
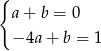
Odejmując od pierwszego równania drugie otrzymujemy 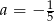 . Stąd
. Stąd 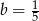 oraz
oraz
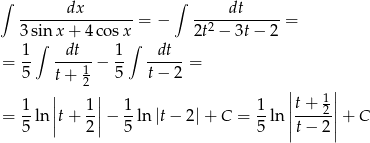
Zatem
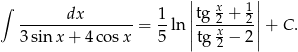
Odpowiedź: