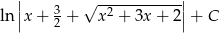Zadanie nr 8632872
Oblicz całkę 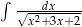 .
.
Rozwiązanie
Będziemy chcieli skorzystać ze wzoru
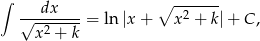
który łatwo jest wyprowadzić stosując podstawienie Eulera 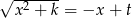 . Aby to zrobić sprowadzamy trójmian pod pierwiastkiem do postaci kanonicznej.
. Aby to zrobić sprowadzamy trójmian pod pierwiastkiem do postaci kanonicznej.
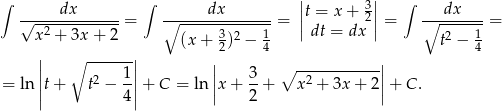
Odpowiedź: 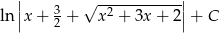
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 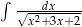 .
.
Będziemy chcieli skorzystać ze wzoru
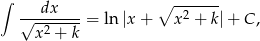
który łatwo jest wyprowadzić stosując podstawienie Eulera 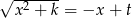 . Aby to zrobić sprowadzamy trójmian pod pierwiastkiem do postaci kanonicznej.
. Aby to zrobić sprowadzamy trójmian pod pierwiastkiem do postaci kanonicznej.
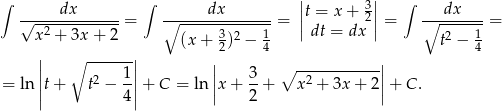
Odpowiedź: