/Szkoła podstawowa/Geometria/Układ współrzędnych

Zadanie nr 1702633

Narysuj w układzie współrzędnych czworokąt o wierzchołkach: 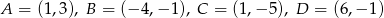A = (1,3), B = (− 4,− 1), C = (1,− 5), D = (6,− 1) , a następnie oblicz jego pole i obwód.

Wersja PDF

Rozwiązanie

Zaznaczamy podane punkty w układzie współrzędnych.

PIC

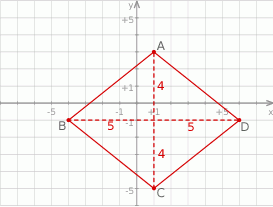
Otrzymany czworokąt to romb. Ponieważ przekątne rombu są prostopadłe i dzielą się na połowy, romb składa się z czterech przystających trójkątów prostokątnych o przyprostokątnych długości 4 i 5. Pole rombu jest więc równe

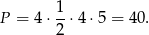
1 P = 4 ⋅--⋅4 ⋅5 = 4 0. 2

Aby obliczyć obwód rombu, obliczamy długość przeciwprostokątnej w jednym z otrzymanych trójkątów (korzystamy z twierdzenia Pitagorasa).

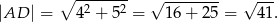
∘ --2----2 √ -------- √ --- |AD | = 4 + 5 = 16+ 25 = 41 .

Obwód rombu jest więc równy

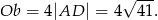
√ --- Ob = 4|AD | = 4 41.

 
Odpowiedź: Pole: 40, obwód: 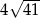√ --- 4 41 .

Wersja PDF