/Szkoła podstawowa/Geometria/Układ współrzędnych

Zadanie nr 5355420

Narysuj w układzie współrzędnych czworokąt o wierzchołkach: 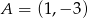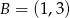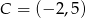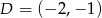A = (1,− 3) , B = (1,3) , C = (− 2,5) , D = (− 2,− 1) , a następnie oblicz jego pole i obwód.

Wersja PDF

Rozwiązanie

Zaznaczamy podane punktu w układzie współrzędnych.

PIC

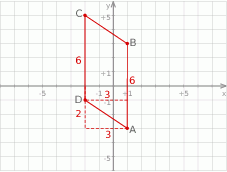
Otrzymany czworokąt to równoległobok o podstawie długości 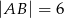|AB | = 6 . Wysokość opuszczona na tę podstawę ma długość 3, więc pole równoległoboku jest równe

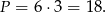
P = 6 ⋅3 = 1 8.

Aby obliczyć obwód równoległoboku stosujemy twierdzenie Pitagorasa do trójkąta prostokątnego, który zaznaczyliśmy przerywaną linią.

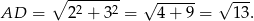
∘ ------- AD = 22 + 32 = √ 4-+-9-= √ 1-3.

Obwód równoległoboku jest więc równy

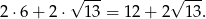
2 ⋅6+ 2⋅√ 1-3 = 12 + 2√ 13.

 
Odpowiedź: Pole: 18, obwód: 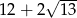√ --- 12 + 2 1 3 .

Wersja PDF