/Szkoła średnia/Zadania testowe/Liczby/Potęgi i pierwiastki/Pierwiastki

Zadanie nr 8488726

Dodaj do ulubionych
Dodaj do rozwiązanych

Wartość wyrażenia 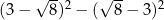√ -- 2 √ -- 2 (3 − 8 ) − ( 8 − 3) jest równa
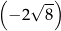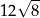A) ( √ -) − 2 8 B) √ -- 12 8 C) 24 D) 0

Rozwiązanie

Sposób I

Zauważmy, że

√ -- [ √ --]2 √ -- ( 8 − 3)2 = − (3− 8) = (3 − 8)2.

Zatem

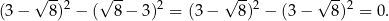
√ -- √ -- √ -- √ -- (3 − 8)2 − ( 8 − 3)2 = (3 − 8)2 − (3 − 8)2 = 0.

Sposób II

Korzystamy ze wzoru skróconego mnożenia na kwadrat różnicy

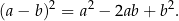
2 2 2 (a− b ) = a − 2ab+ b .

Mamy więc

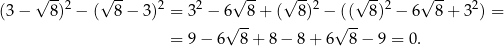
√ -- √ -- √ -- √ -- √ -- √ -- (3 − 8)2 − ( 8 − 3)2 = 32 − 6 8 + ( 8)2 − (( 8)2 − 6 8 + 32) = √ -- √ -- = 9 − 6 8 + 8 − 8 + 6 8 − 9 = 0.

Sposób III

Korzystamy ze wzoru skróconego mnożenia na różnicę kwadratów

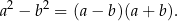
a2 − b2 = (a− b)(a+ b).

Mamy zatem

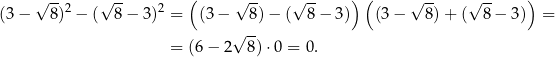
-- -- ( -- -- ) ( -- -- ) (3− √ 8)2 − (√ 8− 3)2 = (3 − √ 8) − (√ 8 − 3) (3 − √ 8 )+ (√ 8 − 3) = √ -- = (6− 2 8) ⋅0 = 0.

 
Odpowiedź: D

Wersja PDF