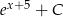/Studia/Analiza/Całki nieoznaczone/Z e^x/Bez ułamka

Zadanie nr 7489369

Oblicz całkę 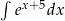∫ x+ 5 e dx .

Wersja PDF

Rozwiązanie

Sposób I

Liczenie całki nieoznaczonej 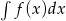∫ f(x)dx to szukanie funkcji 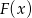F(x ) takiej, że 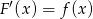F ′(x ) = f(x) . Podany przykład jest na tyle prosty, że możemy funkcję 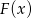F (x) zgadnąć z odpowiednich wzorów na pochodne.

Zgadujemy i sprawdzamy licząc pochodną z prawej strony

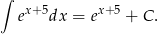
∫ x+5 x+ 5 e dx = e + C.

Sposób II

Jak ktoś jest słaby w zgadywaniu, to może policzyć tę całkę podstawiając 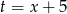t = x + 5 .

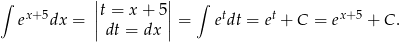
∫ | | ∫ ex+5dx = ||t = x + 5|| = etdt = et + C = ex+5 + C . | dt = dx |

 
Odpowiedź: ex+5 + C

Wersja PDF