Zadanie nr 2954036
Pole prostokąta przedstawionego na rysunku jest równe 20. Zatem

A) 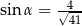 B)
B) 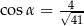 C)
C) 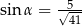 D)
D) 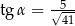
Rozwiązanie
Z podanego pola obliczamy długość drugiego
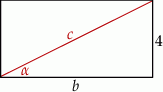
boku prostokąta
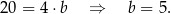
Korzystając z twierdzenia Pitagorasa obliczamy długość przekątnej
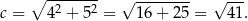
Zatem
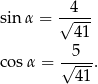
Odpowiedź: A

