/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny/Z parametrem

Zadanie nr 6504252

Dodaj do ulubionych
Dodaj do rozwiązanych

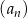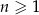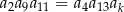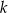Dany jest rosnący ciąg geometryczny (an) , określony dla liczb naturalnych n ≥ 1 , o wyrazach dodatnich. Jeśli a2a9a11 = a4a13ak , to k jest równe
A) 8 B) 7 C) 6 D) 5

Rozwiązanie

Korzystamy ze wzoru 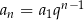n−1 an = a 1q na n –ty wyraz ciągu geometrycznego. Mamy zatem

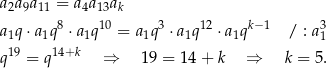
a2a 9a 11 = a4a13ak a q ⋅a q8 ⋅a q10 = a q3 ⋅a q12 ⋅a qk− 1 / : a3 1 1 1 1 1 1 1 q19 = q 14+k ⇒ 19 = 14 + k ⇒ k = 5.

 
Odpowiedź: D

Wersja PDF