/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Różne

Zadanie nr 7828818

Ciąg 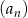(an) dany jest wzorem, 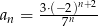3⋅(−-2)n+2 an = 7n . Ciąg 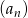(an) jest ciągiem
A) rosnącym B) malejącym C) geometrycznym D) arytmetycznym

Wersja PDF

Rozwiązanie

Jeżeli zapiszemy wzór ciągu w postaci

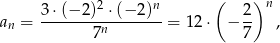
2 n ( )n an = 3-⋅(−-2)--⋅(−-2)- = 12 ⋅ − 2- , 7n 7

to widać, że mamy do czynienia z ciągiem geometrycznym o ilorazie 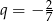q = − 27 . Jeżeli ktoś nie wierzy, to łatwo sprawdzić, że iloraz 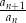an+1- an jest stały (nie zależy od n ):

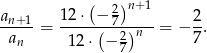
( 2)n+ 1 an+1-= 12-⋅-−(-7-)--- = − 2-. an 12 ⋅ − 27 n 7

Ponieważ iloraz jest ujemny, ciąg ten nie jest monotoniczny. Nie jest to też ciąg arytmetyczny.  
Odpowiedź: C

Wersja PDF