/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Kwadratowy

Zadanie nr 3251513

Ciąg 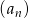(an) określony jest wzorem 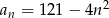2 an = 12 1− 4n , gdzie 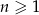n ≥ 1 . Liczba nieujemnych wyrazów tego ciągu jest równa
A) 11 B) 22 C) 10 D) 5

Wersja PDF

Rozwiązanie

Korzystając ze wzoru skróconego mnożenia

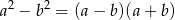
2 2 a − b = (a − b)(a + b)

liczymy

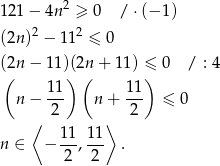
2 121 − 4n ≥ 0 / ⋅(− 1) (2n)2 − 112 ≤ 0 (2n − 11)(2n + 11) ≤ 0 / : 4 ( 1 1) ( 11 ) n − --- n + --- ≤ 0 ⟨ 2 ⟩ 2 11- 11- n ∈ − 2 ,2 .

W takim razie nieujemne wyrazy to: 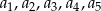a ,a ,a ,a ,a 1 2 3 4 5 .  
Odpowiedź: D

Wersja PDF