Zadanie nr 7111659
Ciąg 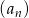 określony jest wzorem
określony jest wzorem 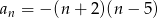 dla
dla 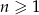 . Zatem
. Zatem
A) 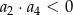 B)
B) 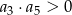 C)
C) 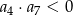 D)
D) 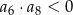
Rozwiązanie
Sposób I
Sprawdźmy, które wyrazy danego ciągu są dodatnie.
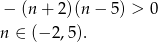
W takim razie dodatnie wyrazy ciągu 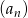 to:
to: 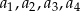 . Ponadto
. Ponadto 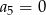 . To oznacza, że wśród podanych warunków tylko
. To oznacza, że wśród podanych warunków tylko 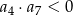 jest prawdziwy.
jest prawdziwy.
Sposób II
Liczymy kilka kolejnych wyrazów danego ciągu.
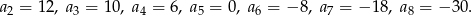
To oznacza, że wśród podanych warunków tylko 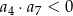 jest prawdziwy.
jest prawdziwy.
Odpowiedź: C

