/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Wymierny

Zadanie nr 2252559

Dodaj do ulubionych
Dodaj do rozwiązanych

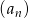Ciąg (an) o wyrazie ogólnym 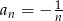1 an = − n jest ciągiem
A) malejącym B) arytmetycznym C) rosnącym D) geometrycznym

Rozwiązanie

Sposób I

Jeżeli pomyślimy jak wyglądają kolejne wyrazy ciągu 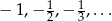1 1 − 1,− 2,− 3,... , to powinno być jasne, że mamy do czynienia z ciągiem rosnącym (liczby są coraz większe).

Sposób II

Sprawdzamy czy ciąg jest geometryczny

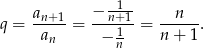
-1-- q = an-+1 = −-n+1-= --n--. an − 1 n + 1 n

Iloraz nie jest liczbą stałą (zależy od n ), więc ciąg nie jest geometryczny. Sprawdzamy czy ciąg jest arytmetyczny

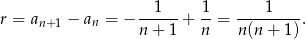
1 1 1 r = an+ 1 − an = − ------+ --= ---------. n + 1 n n (n + 1)

Ponieważ różnica wyrazów ciągu nie jest stałą liczbą, więc ciąg nie jest arytmetyczny. Ponieważ 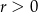r > 0 , więc ciąg jest rosnący.  
Odpowiedź: C

Wersja PDF