/Szkoła średnia/Zadania testowe/Ciągi/Dowolny/Wymierny

Zadanie nr 4769890

Dany jest nieskończony ciąg 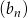(bn) , dla którego 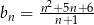n2+5n+-6 bn = n+ 1 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi

Wersja PDF

Rozwiązanie

Sposób I

Licznik i mianownik ułamka definiującego ciąg 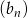(bn) są dodatnie, więc wszystkie wyrazy tego ciągu są dodatnie.

Sposób II

Wyznaczamy pierwiastki licznika

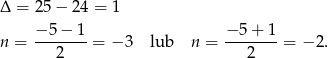
Δ = 25 − 2 4 = 1 n = −-5-−-1 = − 3 lub n = −-5-+-1 = − 2. 2 2

Zatem wzór na ciąg 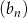(bn) możemy zapisać w postaci

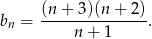
b = (n-+-3)(n-+-2-). n n+ 1

Teraz widać, że wyrazy ciągu 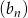(bn) są liczbami dodatnimi i nie muszą to być liczby całkowite.  
Odpowiedź: A

Wersja PDF