/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa/Zbiór wartości

Zadanie nr 4704178

Najmniejsza wartość funkcji 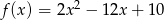2 f(x) = 2x − 12x + 10 w przedziale 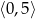⟨0 ,5⟩ jest równa
A) -1 B) -8 C) -10 D) 0

Wersja PDF

Rozwiązanie

Sposób I

Obliczmy pierwszą współrzędną wierzchołka paraboli będącej wykresem funkcji 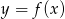y = f(x) .

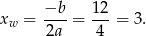
xw = −b--= 12-= 3. 2a 4

Ponieważ punkt ten znajduje się w danym przedziale najmniejszą wartością funkcji w tym przedziale jest

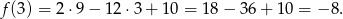
f(3) = 2 ⋅9− 12 ⋅3+ 10 = 18 − 36 + 10 = − 8.

Sposób II

Zapiszmy podaną funkcję w postaci kanonicznej

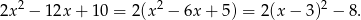
2 2 2 2x − 1 2x+ 10 = 2(x − 6x + 5) = 2(x − 3) − 8.

Widać stąd, że wierzchołek paraboli będącej wykresem tej funkcji ma pierwszą współrzędną równą 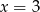x = 3 , czyli w tym punkcie funkcja przyjmuje najmniejszą wartość na przedziale 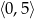⟨0,5⟩ . Wartość ta jest równa f(3) = − 8 .  
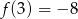Odpowiedź: B

Wersja PDF