/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa/Zbiór wartości

Zadanie nr 6685206

Dodaj do ulubionych
Dodaj do rozwiązanych

Jaka jest najmniejsza wartość funkcji kwadratowej 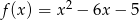2 f(x) = x − 6x− 5 w przedziale ⟨− 3,0 ⟩ ?
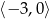A) -14 B) -5 C) -24 D) 5

Rozwiązanie

Sposób I

Policzmy pierwszą współrzędną wierzchołka paraboli będącej wykresem funkcji 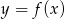y = f(x) .

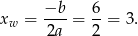
xw = −b-= 6-= 3. 2a 2

Ponieważ punkt ten jest poza danym przedziałem, funkcja przyjmie wartość najmniejszą w jednym z końców przedziału. Sprawdźmy w którym.

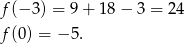
f (− 3) = 9+ 18 − 3 = 24 f (0) = − 5.

Zatem najmniejsza wartość na przedziale 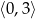⟨0 ,3⟩ to f(0) = −5 .

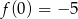Sposób II

Zapiszmy podaną funkcję w postaci kanonicznej

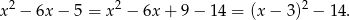
x2 − 6x − 5 = x2 − 6x+ 9− 14 = (x − 3)2 − 14.

Widać stąd, że wierzchołek paraboli będącej wykresem tej funkcji ma pierwszą współrzędną równą 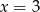x = 3 . Zatem na całym podanym przedziale funkcja maleje (bo ma ramiona skierowane do góry). Zatem najmniejszą wartość przyjmuje w prawym końcu przedziału: f (0) = − 5 .  
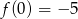Odpowiedź: B

Wersja PDF