Zadanie nr 8650457
Funkcja kwadratowa 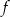 przyjmuje wartość największą równą
przyjmuje wartość największą równą 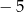 dla argumentu równego 2. Ten warunek spełnia funkcja o równaniu:
dla argumentu równego 2. Ten warunek spełnia funkcja o równaniu:
A) 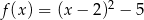 B)
B) 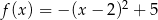
C) 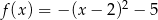 D)
D) 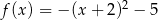
Rozwiązanie
Jeżeli funkcja ma przyjmować wartość największą, to jej wykres musi być parabolą o ramionach skierowanych w dół, czyli współczynnik przy 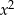 musi być ujemny. Ponadto funkcja kwadratowa postaci
musi być ujemny. Ponadto funkcja kwadratowa postaci
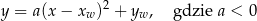
przyjmuje wartość największą 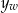 dla
dla 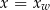 . W takim razie poprawną odpowiedzią musi być
. W takim razie poprawną odpowiedzią musi być
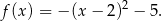
Dla ciekawskich wykres tej funkcji.
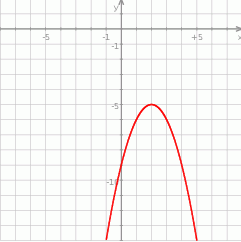
Odpowiedź: C

