Zadanie nr 9820418
Maksymalny zbiór, w którym funkcja kwadratowa 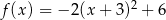 jest rosnąca, to
jest rosnąca, to
A) 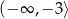 B)
B) 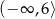 C)
C) 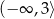 D)
D) 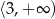
Rozwiązanie
Z podanego wzoru łatwo wyznaczyć współrzędne wierzchołka paraboli będącej wykresem funkcji 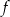
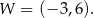
Teraz należy zauważyć, że współczynnik przy najwyższej potędze jest ujemny, więc wykres będzie parabolą zwróconą ramionami w dół. Naszkicujmy wykres (dokładne zaznaczenie pierwiastków nie ma znaczenia dla odczytania przedziałów monotoniczności funkcji)
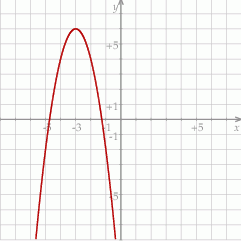
Teraz można łatwo odczytać, że funkcja 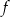 jest rosnąca w zbiorze
jest rosnąca w zbiorze
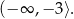
Odpowiedź: A

