/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa/Z parametrem

Zadanie nr 8882136

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa 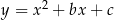2 y = x + bx + c jest malejąca dla 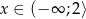x ∈ (− ∞ ;2⟩ , a zbiorem jej wartości jest przedział 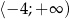⟨− 4;+ ∞ ) . Postać kanoniczna tej funkcji opisana jest wzorem
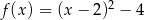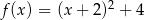
A) f(x ) = (x− 2)2 − 4 B) f(x) = (x+ 2)2 + 4
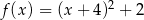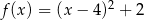
C) 2 f(x) = (x+ 4) + 2 D) 2 f(x ) = (x− 4) + 2

Rozwiązanie

Ponieważ funkcja ma być malejąca w przedziale 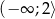(− ∞ ;2⟩ , jej wykresem musi być parabola o ramionach skierowanych w górę i pierwszej współrzędnej wierzchołka równej 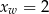xw = 2 . Zbiór wartości będący przedziałem 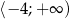⟨− 4;+ ∞ ) oznacza, że druga współrzędna wierzchołka jest równa 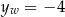yw = − 4 . Dana funkcja ma więc postać kanoniczną:

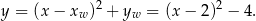
2 2 y = (x− xw) + yw = (x − 2) − 4.

 
Odpowiedź: A

Wersja PDF