Zadanie nr 8097000
Jeżeli 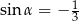 i
i 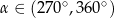 to
to
A) 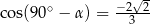 B)
B) 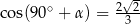
C) 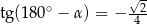 D)
D) 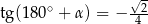
Rozwiązanie
Wiemy, że  jest w 4 ćwiartce, więc jego cosinus jest dodatni. Stąd
jest w 4 ćwiartce, więc jego cosinus jest dodatni. Stąd
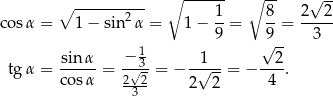
Aby ustalić, która odpowiedź jest poprawna korzystamy ze wzorów redukcyjnych
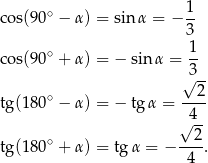
Odpowiedź: D
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Jeżeli 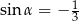 i
i 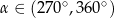 to
to
A) 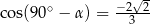 B)
B) 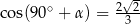
C) 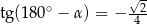 D)
D) 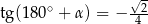
Wiemy, że  jest w 4 ćwiartce, więc jego cosinus jest dodatni. Stąd
jest w 4 ćwiartce, więc jego cosinus jest dodatni. Stąd
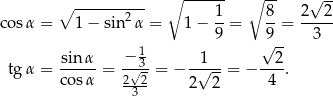
Aby ustalić, która odpowiedź jest poprawna korzystamy ze wzorów redukcyjnych
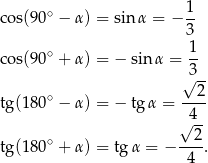
Odpowiedź: D
