/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna/Dany cosinus

Zadanie nr 2076326

Wiadomo, że 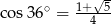∘ 1+√-5 c os36 = 4 . Zatem
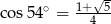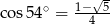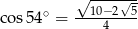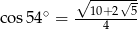
A) √ - cos54∘ = 1+--5 4 B) √- co s54∘ = 1−--5- 4 C) √ ----√-- co s54∘ = --10−4-2-5- D) √ 10+2√-5 cos54 ∘ = ----4----

Wersja PDF

Rozwiązanie

Sposób I

Liczymy

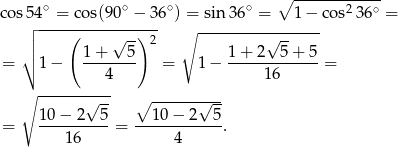
∘ ∘ ∘ ∘ ∘ -------2---∘ cos┌54-=--cos(90--−-3-6 ) = sin 36 = 1 − cos 36 = │ ( √ --)2 ∘ ---------√------- │∘ 1-+---5- 1-+-2--5-+-5- = 1 − 4 = 1 − 16 = ∘ ---------- √ -- ∘ ------√--- = 10-−-2---5 = ---10−--2--5. 16 4

Sposób II

Szkicujemy trójkąt prostokątny o kącie ostrym 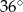∘ 36 .

PIC

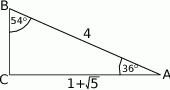
Drugi kąt ostry tego trójkąta ma miarę 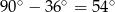90∘ − 36∘ = 54 ∘ . Obliczmy długość drugiej przyprostokątnej

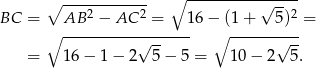
∘ ------------ ∘ ----------√----- BC = AB 2 − AC 2 = 16 − (1 + 5)2 = ∘ ------------------ ∘ ---------- √ -- √ -- = 16 − 1 − 2 5 − 5 = 10 − 2 5.

Zatem

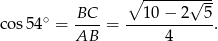
∘ ------√--- ∘ BC-- ---10−--2--5 cos 54 = AB = 4 .

 
Odpowiedź: C

Wersja PDF