Zadanie nr 8874213
Jeżeli wiadomo, że  jest kątem rozwartym i
jest kątem rozwartym i 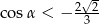 , to
, to 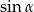 jest liczbą z przedziału
jest liczbą z przedziału
A) 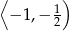 B)
B) 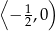 C)
C) 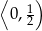 D)
D) 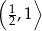
Rozwiązanie
Sposób I
Jeżeli 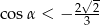 , to
, to
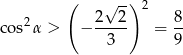
i z jedynki trygonometrycznej
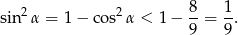
Ponieważ 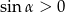 dla kątów rozwartych, mamy stąd
dla kątów rozwartych, mamy stąd
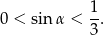
Sposób II
Korzystamy ze wzorów
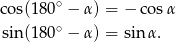
W takim razie kąt ostry 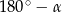 spełnia warunek
spełnia warunek
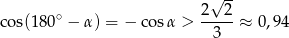
Odczytujemy teraz z tablic, że
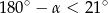
oraz
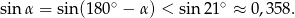
Zatem 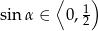 .
.
Odpowiedź: C

