Zadanie nr 5628508
Wielomian 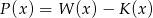 jest siódmego stopnia oraz
jest siódmego stopnia oraz 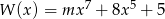 ,
, 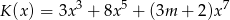 . Wynika stąd, że liczba
. Wynika stąd, że liczba 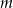 jest różna od
jest różna od
A) 3 B) -1 C) 1 D) 0
Rozwiązanie
Wyznaczamy postać wielomianu 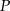
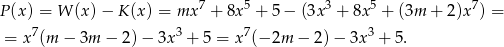
Chcemy żeby wielomian 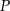 był siódmego stopnia, więc
był siódmego stopnia, więc

Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wielomian 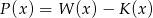 jest siódmego stopnia oraz
jest siódmego stopnia oraz 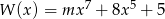 ,
, 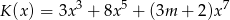 . Wynika stąd, że liczba
. Wynika stąd, że liczba 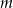 jest różna od
jest różna od
A) 3 B) -1 C) 1 D) 0
Wyznaczamy postać wielomianu 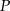
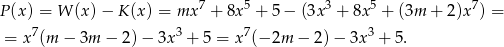
Chcemy żeby wielomian 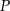 był siódmego stopnia, więc
był siódmego stopnia, więc

Odpowiedź: B
