Zadanie nr 1263707
Miejscami zerowymi funkcji kwadratowej 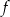 określonej wzorem
określonej wzorem 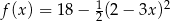 są liczby
są liczby
A) 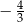 oraz
oraz 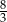 B)
B) 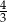 oraz
oraz 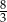 C)
C) 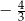 oraz
oraz 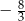 D)
D) 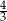 oraz
oraz 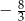
Rozwiązanie
Sposób I
Przekształcamy dany wzór korzystając ze wzoru na różnicę kwadratów
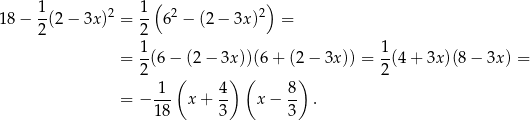
Widać teraz, że miejscami zerowymi tej funkcji są 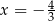 i
i 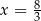 .
.
Sposób II
Rozwiązujemy równanie
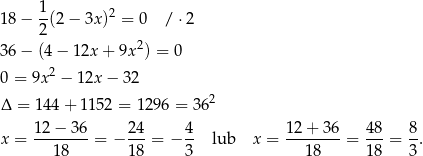
Odpowiedź: A

