/Szkoła średnia/Zadania testowe/Równania/Kwadratowe/Dane równanie

Zadanie nr 4223231

Dodaj do ulubionych
Dodaj do rozwiązanych

Miejscami zerowymi funkcji kwadratowej 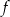f określonej wzorem 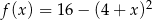f (x) = 16 − (4 + x)2 są liczby
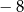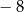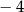A) 0 oraz 4 B) − 8 oraz 8 C) 0 oraz − 8 D) − 4 oraz 4

Rozwiązanie

Sposób I

Przekształcamy dany wzór korzystając ze wzoru na różnicę kwadratów

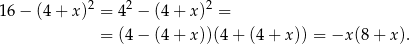
2 2 2 16− (4+ x) = 4 − (4 + x) = = (4 − (4 + x))(4 + (4 + x)) = −x (8+ x ).

Widać teraz, że miejscami zerowymi tej funkcji są 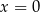x = 0 i x = − 8 .

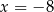Sposób II

Rozwiązujemy równanie

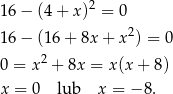
16 − (4 + x)2 = 0 2 16 − (16 + 8x + x ) = 0 0 = x 2 + 8x = x(x + 8) x = 0 lub x = − 8.

 
Odpowiedź: C

Wersja PDF