Zadanie nr 8374531
Liczby 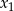 i
i 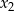 są pierwiastkami równania
są pierwiastkami równania 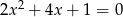 i
i 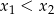 . Oblicz
. Oblicz 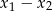 .
.
A) 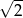 B)
B) 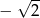 C) -2 D)
C) -2 D) 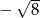
Rozwiązanie
Rozwiązujemy dane równanie
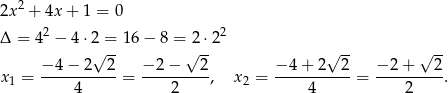
Zatem
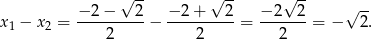
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Liczby 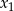 i
i 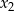 są pierwiastkami równania
są pierwiastkami równania 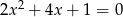 i
i 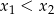 . Oblicz
. Oblicz 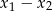 .
.
A) 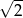 B)
B) 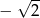 C) -2 D)
C) -2 D) 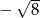
Rozwiązujemy dane równanie
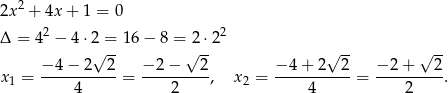
Zatem
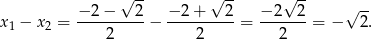
Odpowiedź: B
