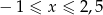/Szkoła podstawowa/Nierówności

Zadanie nr 6120862

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówności i zaznacz na osi liczbowej liczby, które spełniają obie nierówności jednocześnie.

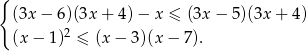
{ (3x− 6)(3x + 4) − x ≤ (3x − 5)(3x + 4) (x− 1)2 ≤ (x − 3)(x − 7).

Rozwiązanie

Rozwiązujemy pierwszą nierówność

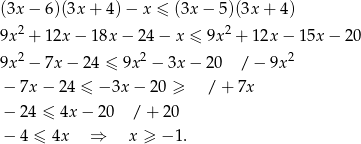
(3x − 6 )(3x+ 4)− x ≤ (3x − 5)(3x + 4) 9x 2 + 1 2x− 18x − 24 − x ≤ 9x2 + 12x − 15x − 2 0 2 2 2 9x − 7x − 24 ≤ 9x − 3x − 2 0 / − 9x − 7x − 24 ≤ − 3x− 20 ≥ / + 7x − 24 ≤ 4x − 20 / + 2 0 − 4 ≤ 4x ⇒ x ≥ − 1.

Teraz rozwiązujemy drugą nierówność

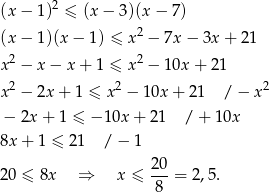
(x− 1)2 ≤ (x− 3)(x − 7) 2 (x− 1)(x− 1) ≤ x − 7x − 3x + 2 1 x2 − x− x+ 1 ≤ x2 − 10x + 21 x2 − 2x+ 1 ≤ x2 − 10x + 2 1 / − x2 − 2x + 1 ≤ − 10x + 21 / + 10x 8x+ 1 ≤ 21 /− 1 20 20 ≤ 8x ⇒ x ≤ ---= 2,5. 8

Szkicujemy teraz zbiór liczb spełniający nierówność 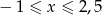− 1 ≤ x ≤ 2,5 .

PIC

 
Odpowiedź: − 1 ≤ x ≤ 2,5

Wersja PDF